Problem Set Key

Turn on library:

library(che302r)
Loading required package: orthopolynom

Problem 1

Compute the momentum and speed of a neutron with a wavelength of \(3 \ mm\). A neutron weighs as much as a proton.

lam <- 3e-3
pN  <- h/lam
pN # momentum of neutron
[1] 2.20869e-31
vN <- pN/mN
vN # speed of neutron
[1] 0.0001318678

Problem 2

Compute the momentum of a photon with a wavelength of \(350 \ nm\). What speed must a hydrogen molecule (H2) travel at to have the same momentum?

lam <- 350e-9
pph <- h/lam
pph # momentum of photon
[1] 1.893163e-27
mH2 <- 2*mP + 2*me
mH2 # mass of hydrogen molecule
[1] 3.347066e-27
pH2 <- pph     # hydrogen molecule momentum is same as photon momentum
vH2 <- pH2/mH2
vH2            # speed of hydrogen molecule
[1] 0.5656187

Problem 3

The speed of a proton is measured to be \(4.5 \times 10^5 \ m/s \pm 1000 \ m/s\). What is the minimum uncertainty in its position?

dv <- 1000
dp <- mP*dv
dp # uncertainty in momentum
[1] 1.672622e-24
dx <-  hb/(2*dp)
dx # uncertainty in position
[1] 3.152451e-11

Problem 4

A \(500 \ W\) green laser (\(525 \ nm\)) is turned on for \(10 \ s\). How many photons does it emit?

lam <- 525e-9
Eph <- h * cl/lam
Eph # Energy per photon
[1] 3.783706e-19

How many mols of photons is this?

# 500 W laser on for 10 s
ph <- 500 * (1/Eph) * 10
ph                       # number of photons spit out in 10s
[1] 1.321456e+22
ph/N.A                   # mols of photons
[1] 0.02194329

Problem 5

A laser emits photons with a wavelength of \(1064 \ nm\) with a power output of \(5 \times 10^6 \ J/s\).

a. Compute the energy form a \(2 \times 10^{-8} \ s\) pulse.
# a.
laser.pow  <- 5e6
pulse.time <- 2e-8
laser.pow * pulse.time
[1] 0.1
b. Compute the energy of one photon from this laser.
#b.
lam <- 1064e-9
Eph <- h * cl/lam
Eph # Energy per photon
[1] 1.86696e-19
# **** alternative solution for a. since we now know the energy per photon from b. ****
# 5e6 W laser on for 2e-8 s
ph <- 5e6 * (1/Eph) * 2e-8
ph # number of photons spit out in 2e-8 s pulse
[1] 5.3563e+17
Eph * ph # Energy in the 2e-8 s pulse
[1] 0.1
c. Compute the number of photons in 10 pulses.
#Laser power (J/s) / energy per photon (J/ph) * pulse time (s) * 10 pulses:
laser.pow * (1/Eph) * pulse.time * 10 # Number of photons in 10 pulses:
[1] 5.3563e+18

Problem 6

The work function for metallic Cesium is \(2.14 \ eV\). Compute the K.E. and speed of and electron hit by a photon of wavelength \(300 \ nm\). What if the wavelength of the photon is \(600 \ nm\)?

Phi    <- 2.14              # Work function in eV
lambda <- 300e-9            # Photon wavelength
#lambda <- 600e-9           # The other Photon's wavelength

PhiJ <- Phi * 1.602177e-19 # Convert Phi to Joules
Eph  <- h * cl/lambda      
Eph                        # Energy of the photon
[1] 6.621486e-19
KEe <- Eph - PhiJ
KEe                        # KE of the kicked out e-
[1] 3.192827e-19

Problem 7

The work function for metallic Francium is \(3.84 \ eV\) \((1 \ eV = 1.602677 \times 10^{-19} J)\). Compute the K.E. and speed of and electron hit by a photon of wavelength \(170 \ pm\). What if the wavelength of the photon is \(170 \ \mu m\)?

Phi    <- 3.84              # Work function in eV
lambda <- 170e-12           # Photon wavelength
#lambda <- 170e-6           # Photon wavelength
me     <- 9.1093837015e-31  # Mass e-

PhiJ <- Phi * 1.602177e-19 # Convert Phi to J
Eph  <- h * cl/lambda

# KE of the kicked out e-
KEe <- Eph - PhiJ
KEe
[1] 1.167882e-15
# Speed of the kicked out e-
ve <- sqrt(2*(Eph - PhiJ)/me)
ve
[1] 50637242

Problem 8

Compute the DeBroglie wavelength of an electron accelerated through a potential of \(134 \ V\) (\(1 \ V = 1 \ J/C\)).

# 1e- accelerated by 134V
# 1V = 1J/C
Eelec <- 134 * ec # ec = charge of an electron in Coulombs
Eelec             # energy of an electron accelerated through 134V potential
[1] 2.146917e-17
# From E=hc/lambda and p=h/lambda:
pelec <- Eelec/cl
pelec             # momentum of the electron
[1] 7.161343e-26

Problem 9

The fourth fringe of an interference pattern formed by a beam of electrons traveling through a double slit mask appears at \(3.3^{\text{o}}\) to incidence. If the slits are \(0.5 \ mm\) apart, compute:

a. the wavelength of the particles in nm:
n      <- 4            # Fringe index
d      <- 0.5e-3       # Slit spacing
theta  <- 3.3 * pi/180 # Angle

# a. n lambda = d sin(theta)
lambda <- d*sin(theta)/n
lambda     # wavelength in m
[1] 7.195503e-06
lambda*1e9 # wavelength in nm
[1] 7195.503
b. the energy of the particles (mks units!):
# b. E = hc/lambda
E <- h*cl/lambda
E # energy in J
[1] 2.760677e-20
c. the momentum of the particles (mks units!):
# c. p = h/lambda
p <- h/lambda
p # momentum in kg m/s
[1] 9.208626e-29
d. If the average speed of particles in the beam is 100 m/s compute the average particle mass (mks units!):
# d. p = mv
v <- 100
m <- p/v
m # mass in kg
[1] 9.208626e-31

Problem 10

If the minimum uncertainty in the position of an electron on a straight wire is \(150 \ pm\) compute the minimum uncertainty in its momentum and speed.

dx <- 150e-12
dp <- hb/(2*dx)
dp              # minimum uncertainty in momentum
[1] 3.515239e-25
dv <- dp/me
dv              # minimum uncertainty in speed
[1] 385892.1

Problem 11

The Heisenberg uncertainty relation for energy and time is:

\[\Delta E \Delta t \geq \frac{\hbar}{2}\]

If the uncertainty in the lifetime of an excited state is \(1 \times 10^{-9} \ s\) what is the uncertainty in the state’s energy?

dt <- 1e-9
dE <- hb/(2*dt)
dE
[1] 5.272859e-26

Problem 12

Sketch a black body curve for \(T = 100 \ K\), \(T = 1000 \ K\) and \(T = 10000 \ K\). Label the axes.

1. Black body for \(T = 100 \ K\):
k100   <- planck.distribution(x.min = 0.1e-9, x.max = 200000e-9, Temp = 100, typ = "wavelength", plotQ = T)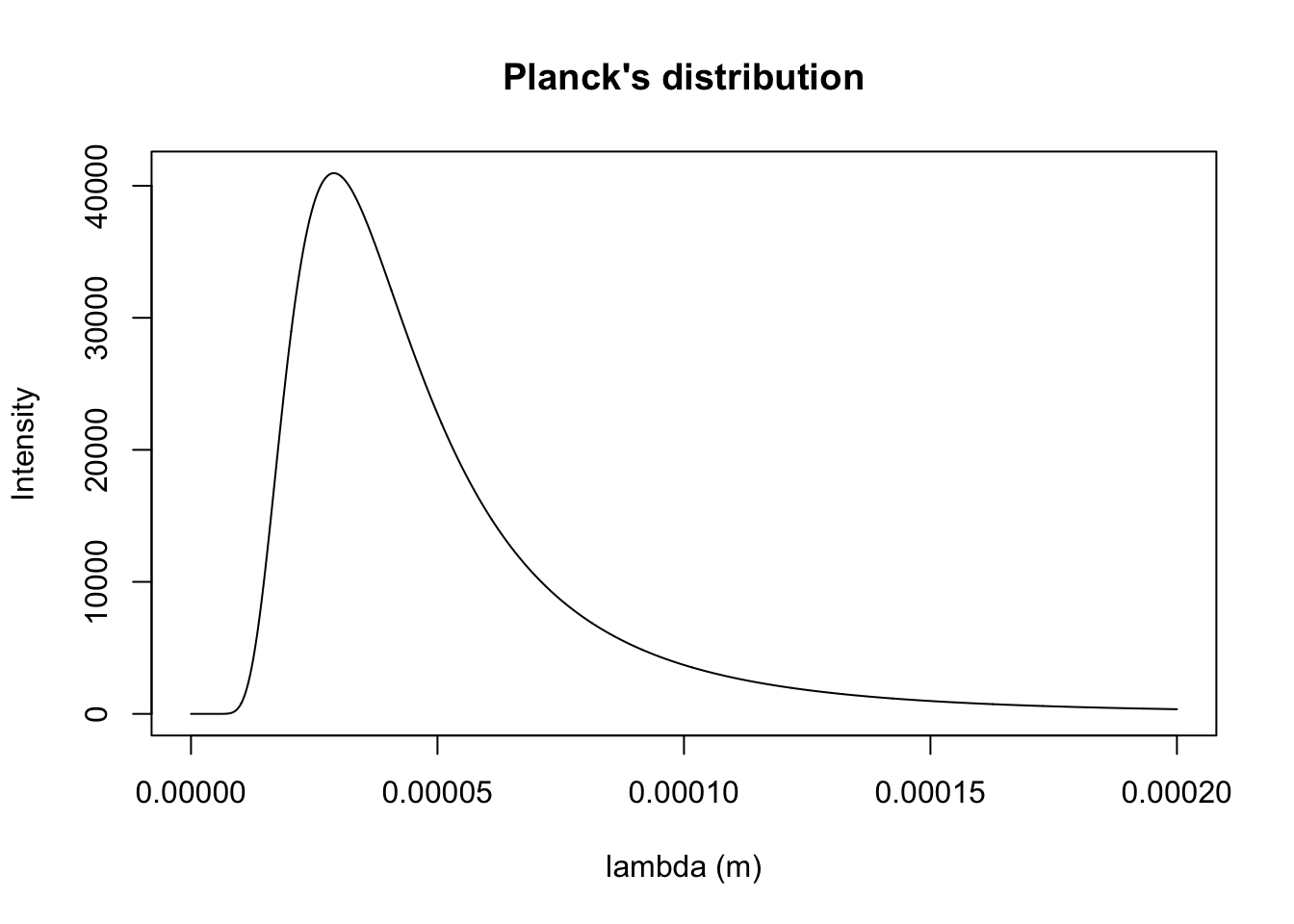

2. Black body for \(T = 1000 \ K\):
k1000  <- planck.distribution(x.min = 0.1e-9, x.max = 200000e-9, Temp = 1000, typ = "wavelength", plotQ = T)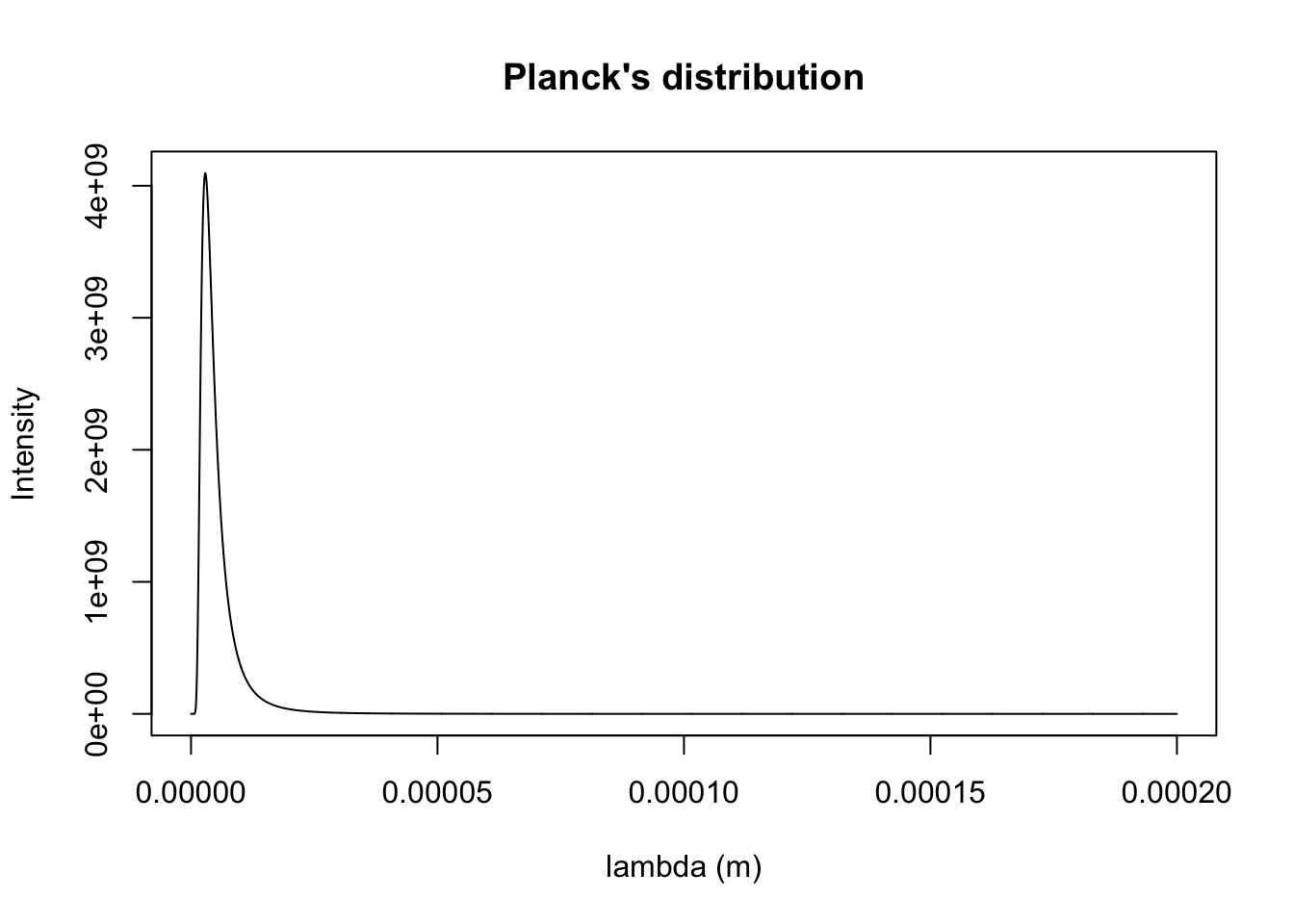

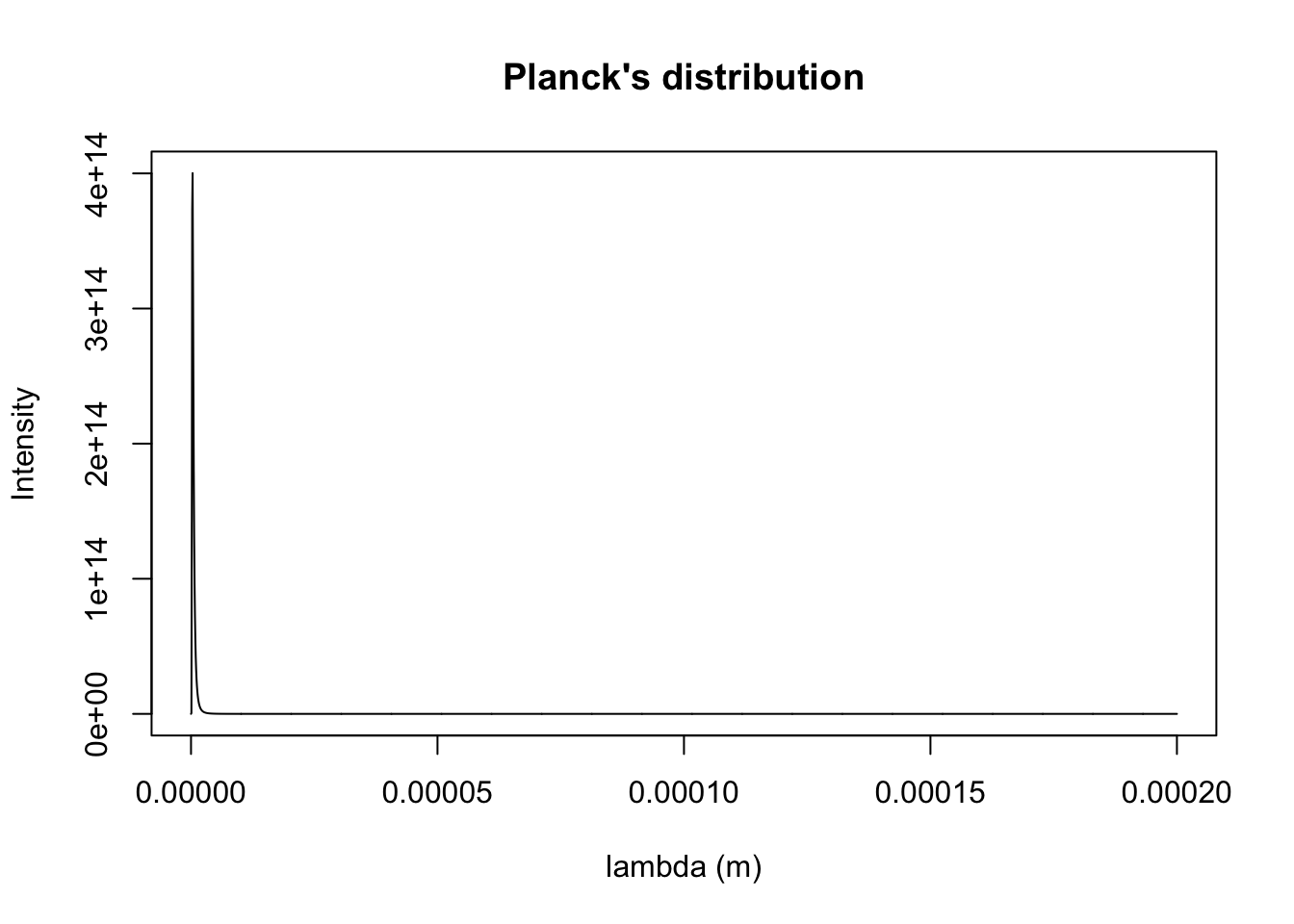
3. Black body for \(T = 10000 \ K\):
k10000 <- planck.distribution(x.min = 0.1e-9, x.max = 200000e-9, Temp = 10000, typ = "wavelength", plotQ = T)